ГОСТ 24346-80 «Вибрация. Термины и определения» определяет вибрацию как «движение точки или механической системы, при котором происходят колебания характеризующих его скалярных величин». Колебания скалярной величины объясняются как «процесс поочередного возрастания и убывания во времени значений какой-либо величины».
Под это определение попадают множество колебательных процессов, начиная с вращения планет вокруг Солнца, заканчивая колебаниями электронов на орбитах движения вокруг ядра. Световые волны, которые позволяют нам видеть, имеют колебательную природу. Морские приливы также являются колебаниями. Окружающий мир, во многом состоит из колебаний.
Вибрация для механического оборудования может быть:
- полезной – для вибрационных грохотов, бетоноуплотнительных машин, разгрузочных вибраторов железнодорожных вагонов, вибрационных трамбовок, виброшлифовальных машин и другой вибрационной техники;
- разрушительной – для механизмов роторного типа, транспортной техники, двигателей внутреннего сгорания и электрических двигателей, металлообрабатывающего оборудования, металлургических машин, зданий и сооружений и др.;
- источником информации о техническом состоянии‑этот информационный аспект составляет основу вибрационной диагностики и данного учебника.
Необходимость измерения вибрации машин возникла во второй половине XIX века. Это связано с появлением паровых судов, имеющих лёгкие по сравнению с наземными сооружениями конструкции и мощные приводные машины. Возникновение вибрации всегда неприятно для экипажа и пассажиров. Последствия вибрации – аварии из-за поломок деталей механизмов, значительно снижали доверие к этому новому, в то время виду транспорта. Часто интенсивные колебания наблюдались в подвижном составе развивающегося железнодорожного транспорта.
Вначале, для регистрации вибрации использовались органолептические методы, основанные на визуальных или тактильных ощущениях. Значения параметров вибрации субъективно оценить затруднительно. При возможности сравнительного анализа точность оценки амплитуды вибрации не превышает 20%. Абсолютная оценка всегда содержит грубые ошибки из-за нераспознанного спектрального состава вибрации. В высокочастотном диапазоне возможности человека по восприятию вибрации ограничены. Надёжным виброметром человек служить не может.
Наибольшая чувствительность при воздействии вибрации на человека наблюдается при частоте 100…300 Гц. Распознать частоту колебаний практически невозможно, если эти колебания происходят с частотой свыше 5 Гц. Однако, человек ощущает дискомфорт, находясь рядом с машиной генерирующей частоты, совпадающие с резонансными частотами частей человеческого тела.
Если колебания настолько редки, что глаз различает каждое из них в отдельности, то частота определяется подсчётом полных колебаний за некоторый промежуток времени. С уменьшением размаха колебаний точность глазомерного восприятия уменьшается. Частота колебаний в диапазоне 25…100 Гц позволяет различить малые амплитуды до 0,1 мм.
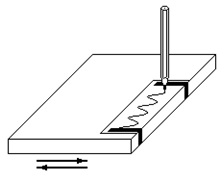
Подтверждением присутствия вибрации становились различные методы визуализации механических колебаний. Размах больших колебаний (5 мм и выше) можно определить по отбрасываемой объектом тени на экран в пучке параллельных либо расходящихся лучей. Характер прямой линии, проведенной по бумаге, лежащей на корпусе механизма, позволяет качественно оценить частоту и интенсивность колебаний (рисунок 58а). При этом регистрируются колебания в направлении перпендикулярном направлению движения карандаша. Скорость перемещения карандаша должна быть как можно более постоянной.
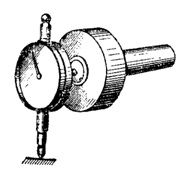
Часто, для измерения размаха виброперемещения машин и балансировочных станков применялись ручные виброметры с использованием индикатора часового типа (рисунок 58б). Размах колебаний вибрирующей поверхности, с которой соприкасается стержень индикатора, определяется по размаху колебаний стрелки индикатора. При сильных вибрациях такие виброметры быстро выходят из строя.
Рисунок 58 – Пример «ручной» записи механических колебаний (а), общий вид ручного виброметра с использованием индикатора перемещения часового типа (б)
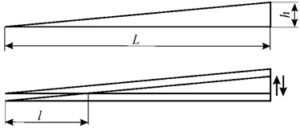
В случае необходимости регистрации относительно больших амплитуд колебаний (0,5…10 мм) с точностью до 0,5 мм при малой частоте (10…20 Гц) возможно применение мерного клина. При вибрации, происходящей с частотой 8 Гц и выше в направлении перпендикулярном колебаниям (рисунок 59а), глаз сохраняет способность зрительного восприятия всех положений клина и четко видит точку пересечения крайних положений клина на расстоянии l от начала треугольника. Если размах колебаний s, высота клина h и основание L, то из подобия треугольников:
Рисунок 59 – Визуализация механических колебаний:
а) схема измерения амплитуды колебаний при помощи мерного клина; б, в) пример установки мерного клина на оборудовании; г) контроль уровня вибрации гидроагрегата при помощи монеты
Мерный клин (рисунок 59б) наклеивается на корпус диагностируемого механизма. Наличие пространственных компонентов вибрации, действующих перпендикулярно к измеряемой плоскости, может исказить результат. Поэтому мерный клин применяется главным образом для измерения прямолинейной вибрации, в частности колебаний: сит, грохотов, вибростендов и т.п.
Для сравнения размаха колебаний в вертикальной плоскости возможно использование мелких вспомогательных предметов. Различное поведение монет, гаек, шайб в различных местах механизма, сухого мелкого песка на горизонтальной поверхности поможет выявить узлы с наибольшей вибрацией. Характерный пример – установка монет на ребро (рисунок 59г).
Виды колебательных процессов
Вибрация‑ это механические колебания или повторяющееся движение объекта около положения равновесия. Вибрация тела вызывается силами возбуждения. Эти силы прикладываются к объекту извне или возникают внутри него.
Колебательные процессы следует разделить на стационарные и нестационарные. Нестационарные колебания разделяются на длительные, кратковременные и переходные. Пример переходного процесса ‑ вибрация механизма при разгоне или при остановке и выбеге. Кратковременные процессы – подъём груза мостовым краном или перемещение крана. Длительные нестационарные процессы соответствуют режиму работы прокатных клетей или скипового подъёмника доменной печи, когда нагрузка изменяется при выполнении технологических операций.
Стационарные процессы имеют постоянные во времени параметры. Общий уровень, распределение амплитуд и частот, составляющих вибрации для стационарных процессов остаются практически неизменными в кратковременном интервале – как минимум в течение нескольких часов. Данные процессы наиболее характерны для механизмов роторного типа.
Стационарные процессы подразделяются на периодические и случайные.
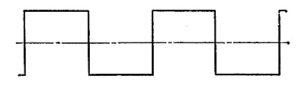
Периодические колебания представляют собой колебания, при которых каждое значение колеблющейся величины повторяется через равные интервалы времени – периоды (рисунок 60).
 |
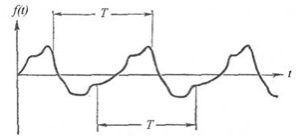 |
Рисунок 60 – Примеры периодических колебаний
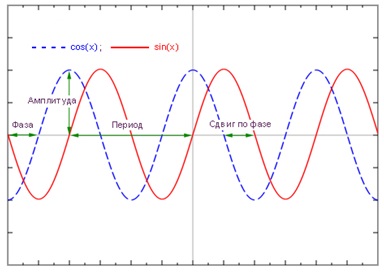
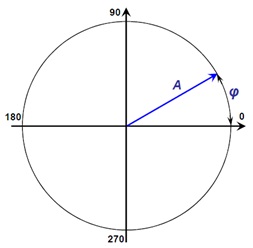
Одним из видов периодических колебаний являются гармонические колебания – колебания, при которых значения колеблющейся величины изменяются во времени по закону синуса или косинуса (рисунок 61):
S(t) = А·sin(wt + j),
S(t) = А·cos(wt + j),
где А – амплитуда колебаний (мм); t – время (сек); j – начальная фаза колебаний (рад); w – угловая скорость (рад/сек); wt + j – фаза колебания (рад).
Амплитуда колебания А – максимальное отклонение колеблющегося параметра от среднего значения. Фаза wt+j определяет состояние колебательного процесса в определенный момент времени t. Начальная фаза j характеризует состояние колеблющейся системы в начальный момент времени t = 0.
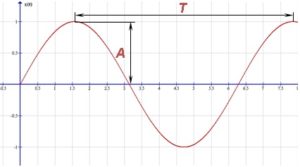
Периодом колебаний T называется наименьший промежуток времени, через который колеблющаяся система возвращается к исходному состоянию.
Частотой колебаний f называется число колебаний за одну секунду. Если T — период колебаний, то f = 1/T. Частота измеряется в герцах (Гц) – одно колебание в секунду. Одно полное колебание (2π радиан), синусоида совершает за период Т, следовательно, угловая скорость (или частота) w = 2π / Т = 2πf.
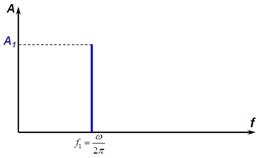
Формы представления гармонических колебаний приведены на рисунке 62.
|
x(t) = A × sin(wt + j0) Математические зависимости |
|
Рисунок 62 – Формы представления гармонических колебаний
При гармонических колебаниях: А, w, j = const.
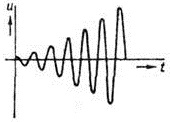
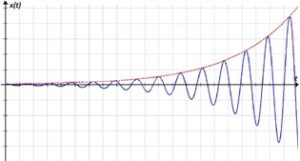
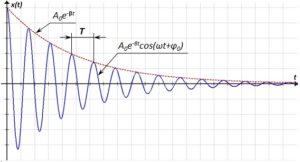
При почти гармонических (квазигармонических) колебаниях: А, w, j – меняющиеся функции времени, некоторые из них могут быть постоянными, некоторые возрастающими или убывающими (рисунок 63). Например, амплитуда, угловая скорость при запуске либо при остановке механизма создают затухающие или возрастаающие колебания ‑ колебания с убывающей или возрастающей со временем амплитудой:
X(t)=A0e—βtcos(ωt+φ0) или X(t)=A0eβtcos(ωt+φ0)
где β – коэффициент затухания.
Рисунок 63 – Квазигармонические колебания
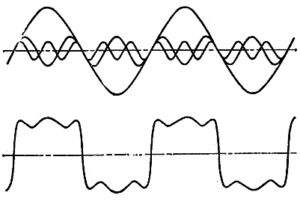
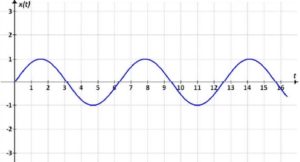
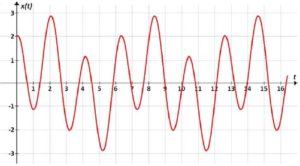
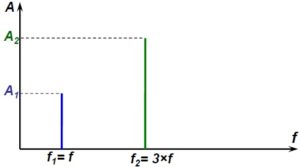
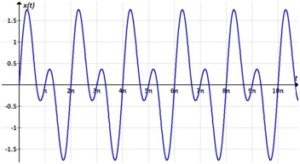
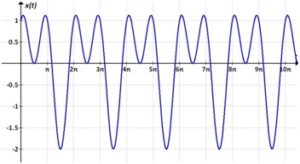
Полигармонические колебания – колебания, которые могут быть представлены в виде суммы двух или более гармонических колебаний (гармоник), частоты которых кратны основной частоте (рисунок 64).
 |
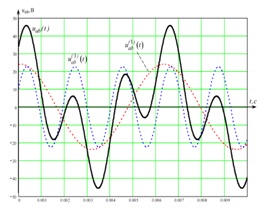 |
Рисунок 64 – Полигармонические колебания
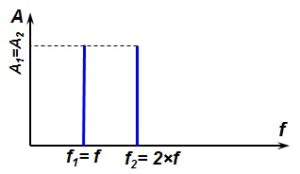
Форма полигармонических колебаний существенно зависит от сдвига начальных фаз складываемых гармоник, при этом в спектральном представлении отличия отсутствуют (рисунок 65).
 |
|
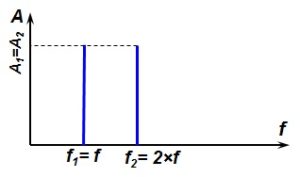 |
Рисунок 65 – Сложение гармонических колебаний с разной фазой
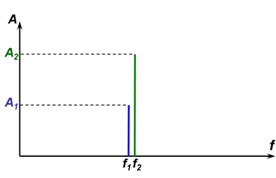
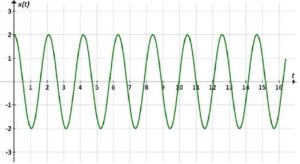
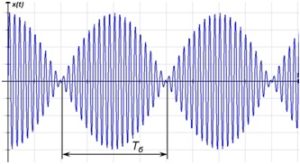
Одним из видов полигармонических колебаний являются биения – сложение двух гармонических колебаний с близкими частотами (рисунок 66).
 |
|
Рисунок 66 – Биения
Время между точками А и В определяет момент когда число циклов колебаний одной частоты будет на единицу превышать число циклов колебаний другой частоты. Общая амплитуда колебаний в эти моменты равна нулю. Чем меньше разность частот двух составляющих, тем больше длина интервала АВ. В середине интервала общая амплитуда соответствует сумме амплитуд колебаний.
Случайные процессы – непредсказуемы по своему частотному составу и уровням амплитуд, но сохраняют свои статистические характеристики (среднее значения, дисперсию) на протяжении процесса наблюдения. Например: кавитация в проточной части насоса, повреждения подшипников качения, силы трения в подшипниках качения и скольжения, турбулентность в потоке газа или жидкости и др.
Колебательные процессы можно разделить на типы в зависимости от источников энергии в этих процессах:
- свободные или собственные колебания – определяются внутренними параметрами деталей, их массой и жёсткостью, возникающие за счёт однократного внешнего воздействия на систему (после выведения системы из состояния равновесия, за счёт сообщенной энергии из вне), в реальных условиях свободные колебания всегда затухающие;
- вынужденные колебания – вызываются и поддерживаются переменным внешним воздействием (вибрация роторного механизма, вызванная дисбалансом), при периодическом поступлении энергии из вне к колебательной системе;
- параметрические колебания – вызываются изменением динамических параметров системы (жёсткости, массы или момента инерции, демпфирования и др.), в результате внешнего воздействия;
- автоколебания – незатухающие колебания в динамической системе, поддерживающиеся за счёт энергии непериодического внешнего воздействия;
- случайные колебания, возникают в результате случайных внешних воздействий и (или) из-за случайных параметров системы;
- крутильные колебания возникают при неравномерном вращении вала.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы. Например:
- колебания маятника часов за счёт действия тяжести заводной гири;
- колебания скрипичной струны под воздействием движущегося смычка;
- работа электрического звонка и др.
Вибрацию также классифицируют: по её природе (механическая, аэрогидродинамическая, электромагнитная, электродинамическая); по конструктивному узлу (элементу) её вызывающему (роторная, лопаточная, подшипниковая, зубчатая).
Модель – это такой материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале.
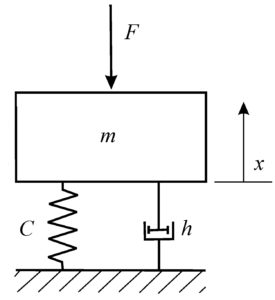
Вибрационные характеристики механизма определяются параметрами внешнего нагружения и внутренней структуры взаимодействия узлов и деталей. Изучение вибрационной картины механизма начинается с универсальной расчётной модели отдельного элемента, показанной на рисунке 67.
 |
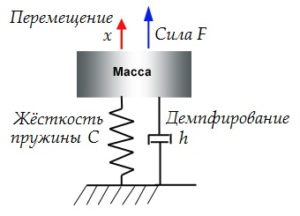 |
Рисунок 67 – Расчётная модель возникновения колебаний
Компонентами данной модели являются:
- Сила F – векторная физическая величина, являющаяся мерой интенсивности воздействия на тело других тел, а также полей. Приложенная к телу сила является причиной изменения его скорости или возникновения в нём напряжений.
Сила как векторная величина характеризуется модулем, направлением и точкой приложения силы. Для возникновения колебаний сила должна быть переменной по модулю или по направлению. Этому требованию отвечают:- силы механической природы: центробежные, кинематические, параметрические, динамические, силы трения, силы ударного взаимодействия;
- силы электромагнитного происхождения: магнитные, электродинамические, магнитострикционные – определяемые изменением линейных размеров магнитного материала под действием магнитного поля;
- силы аэродинамического происхождения: подъёмные силы, силы трения на границе потока и неподвижных частей машины, пульсации давления в потоке;
- силы гидродинамического происхождения – имеют ту же природу, что и в газовой среде, но к ним добавляются пульсации давления из-за кавитации.
Сила упругости – сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное состояние (противодействует деформации).
Сила инерции – векторная величина, численно равная произведению массы m материальной тела на его ускорение и направленная противоположно ускорению.
Сила трения – это сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению.
- Масса – скалярная физическая величина, характеризующая инертность тела и определяющая вес тела при взаимодействии с гравитационными полями.
- Жёсткость – это способность конструктивных элементов сопротивляться деформации при внешнем воздействии. Основной характеристикой жёсткости является коэффициент жёсткости, равный силе, вызывающей единичное перемещение в точке приложения силы.
- Демпфирование – способность к подавлению колебаний (способность к рассеиванию энергии колебаний).
Уравнение движения для данной модели выглядит следующим образом:
Первый компонент данного уравнения соответствует второму закону Ньютона, второй указывает на поглощение колебаний, а третий – закон Гука.
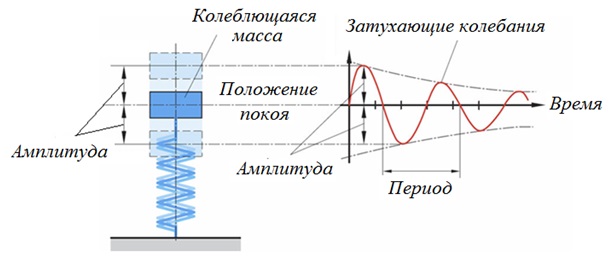
Основной характеристикой расчётной модели является частота собственных колебаний. Собственные колебания — это колебания в системе под действием внутренних сил после того, как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Примером свободных колебаний являются колебания груза, прикреплённого к пружине (рисунок 68).
Частота собственных колебаний определяется массой и жёсткостью:
Поэтому, объекты большой массы имеют собственную частоту колебания на низких частотах, а объекты, имеющие высокую жёсткость, имеют собственную частоту колебания на высоких частотах.
При совпадении частоты собственных колебаний с частотой колебаний вынуждающей силы возникает резонанс – явление резкого возрастания амплитуды вынужденных колебаний. Резонансные явления могут вызвать разрушения в механических системах. Для роторных машин важной характеристикой является критическая скорость – частота вращения вала двигателя, при которой возникает повышенная вибрация из-за совпадения частот вынужденных и собственных колебаний. Амплитуда колебаний при этом повышена, но не бесконечна из-за демпфирования колебаний элементами механической системы. При резонансе происходит изменение фазы на 900 между силой, вызвавшей резонанс, и реакцией системы.
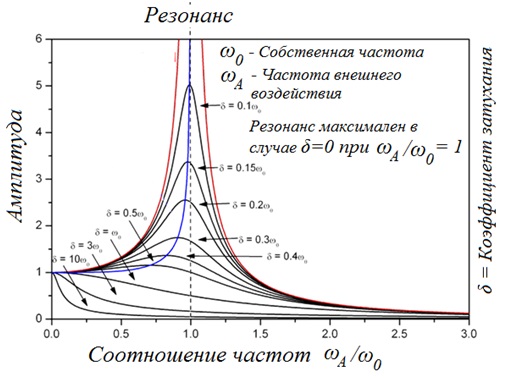
Прикладывая периодическую силу постоянного значения, которая увеличивается по частоте и записывая амплитуду перемещения при различных значениях коэффициента затухания (коэффициент затухания δ= h/2m), получаем частотные характеристики классической системы (рисунок 69).
При низких частотах возбуждения (рисунок 69), амплитуда колебаний почти не изменяется. При совпадении частоты собственных и вынужденных колебаний амплитуда достигает максимального значения, при малом демпфировании. При увеличении демпфирования значение амплитуды снижается. При максимальном демпфировании на частотной характеристике практически нет пика – система сильно демпфирована. С увеличением частоты возбуждения амплитуда уменьшается. Эти свойства частотных характеристик наблюдаются и на вращающихся системах.
Вопросы для самостоятельного контроля
- Может ли человек работать надёжным виброметром?
- Зачем используется «мерный клин»?
- Какие существуют виды колебательных процессов?
- Что такое биения?
- Какие основные компоненты включает расчётная модель колебаний?
- Что такое и как определяется частота собственных колебаний?
- В каких случаях наступает резонанс?




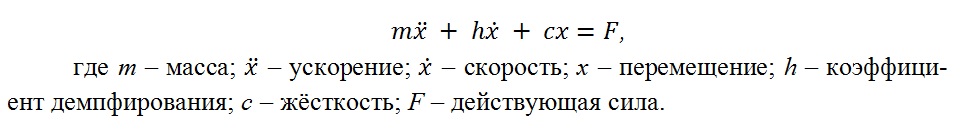
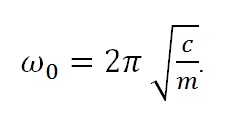
Пока нет комментариев