2.3. Вибрация механизмов

Механическое оборудование: техническое обслуживание и ремонт / В.И. Бобровицкий, В.А. Сидоров. — Донецк: Юго-Восток, 2011. — 238 с.

Наиболее информативным методом получения данных о техническом состоянии механического оборудования в настоящее время является анализ параметров вибрационного сигнала. Для решения различного уровня практических и исследовательских задач используются:

• анализ шумов механизмов;
• измерение общего уровня вибрации;
• измерение параметров вибрации;
• анализ спектра вибрационного сигнала и анализ временных реализаций [8].

Предварительно рассмотрим природу возникновения механических колебаний на примере одномассовой системы (рисунок 2.6). Параметрами данной системы являются:

• масса (m);
• жёсткость (c);
• коэффициент демпфирования (h).

Колебания системы возможны при воздействии силы (F), переменной относительно направления колебаний. Сила F может быть и постоянной, однако параметры контактирующих поверхностей могут служить причиной её периодического изменения. Например, сила тяжести при взаимодействии с изношенной поверхностью подшипника при вращении вала служит источником колебаний. Частотная характеристика колебаний укажет на характер повреждения.

Параметры колебательного процесса определяются следующим уравнением, в котором k — частота собственных колебаний системы, ε — параметр, определяющий демпфирующие свойства системы:

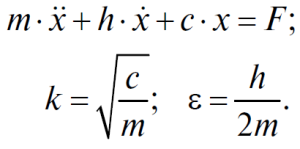Повреждения в механической системе могут приводить к изменению:

• жёсткости (например, износ деталей, ослабление резьбовых соединений);
• коэффициента демпфирования (в случае появления трещин);
• воздействующих сил (при изменении шероховатости контактирующих поверхностей).

Вибрационные процессы можно разделить на стационарные (определённые во времени) и нестационарные (не определённые во времени). Стационарные процессы могут быть периодическими, гармоническими или полигармоническими и непериодическими — почти периодическими, переходными, а также случайными. Периодические колебания — колебания, при которых каждое значение колеблющейся величины повторяется через равные интервалы времени. Простейший периодический сигнал — гармоническое колебание.

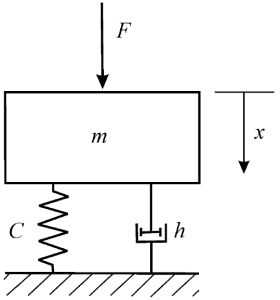
Гармонические колебания — колебания, при которых значения колеблющейся величины изменяются во времени по закону синуса или косинуса (рисунок 2.7):

S(t) = A × sin(ω × t + φ),

где А — амплитуда колебаний; φ — начальная фаза колебаний; ω — угловая скорость.

При гармонических колебаниях: А, φ, ω = сonst. При почти гармонических колебаниях: А, φ, ω — медленно меняющиеся функции времени, некоторые из них могут быть постоянными, некоторые возрастающими или убывающими. Например, амплитуда, угловая скорость при запуске либо при остановке механизма.

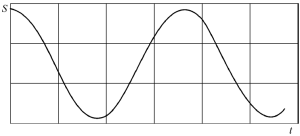
Полигармонические колебания могут быть представлены в виде суммы двух или более гармонических колебаний (гармоник), частоты гармоник кратны основной частоте (рисунок 2.8).

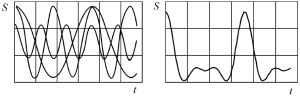
Случайные процессы непредсказуемы по своим параметрам (частоте, амплитуде), но сохраняют свои статистические характеристики (среднее значение, дисперсию) на протяжении всего процесса наблюдения. Например: кавитация в проточной части насоса, шум работающего двигателя.

Нестационарные процессы разделяются на непрерывные и кратковременные. Это процессы, вероятностные характеристики которых являются функциями времени. Например: ударные процессы, проявление повреждений, трещин в процессе работы.

Вибрацию классифицируют:

• по природе:
  • механическая;
  • аэрогидродинамическая;
  • электромагнитная;
  • электродинамическая);
• по конструктивному узлу:
  • роторная;
  • лопаточная;
  • подшипниковая;
  • зубчатая.

Параметры периодических колебаний

1. Частота вибраций:

   f = 1 / T (Гц),

   где Т — период (время полного цикла колебаний), с; ω = 2 × π × f — угловая скорость. Позволяет идентифицировать источник вибрации, повреждения.

2. Виброперемещение S (мкм) — составляющая перемещения, описывающая вибрацию. Виброперемещение как диагностический параметр представляет интерес в тех случаях, когда необходимо знать относительное смещение элементов объекта или деформацию.
3. Виброскорость V (мм/с) — производная виброперемещения по времени. Виброскорость используют при определении технического состояния машин при измерении общего уровня вибрации. Этот параметр связывают с энергией механических колебаний, направленной на разрушение деталей.
4. Виброускорение а (м/с²) — производная виброскорости по времени. Виброускорение используют при определении степени повреждения и силы ударов в подшипниках качения и зубчатых передачах.

Взаимосвязь колебательных величин при гармонических процессах:

S = V × 10³ / (2 × π × f) = a × 10⁶ / (2 × π × f)²;
V = 2 × π × f × S × 10^-3 = a × 10³ / (2 × π × f);
a = (2 × π × f)² × S × 10^-6 = 2 × π × f × V × 10^-3.

Основные характеристики колебательных, вибрационных процессов

Размах колебаний — разность между наибольшим и наименьшим значениями колеблющейся величины в рассматриваемом интервале времени (двойная амплитуда).

Пиковое значение — определяется как наибольшее отклонение колебательной величины от среднего положения.

Среднеарифметическое мгновенных значений вибрации характеризует общую интенсивность вибрации.

Среднее квадратичное значение — квадратный корень из среднего арифметического или среднего интегрального значения квадрата колеблющейся величины в рассматриваемом периоде времени.

Коэффициент амплитуды (пикфактор) — отношение пикового значения к среднеквадратичному значению измеряемого параметра.

Измерения виброперемещения (пиковое или амплитудное, размах колебаний) проводят в низкочастотном диапазоне 2-400 Гц. Ориентировочные значения виброперемещения указаны в таблице 2.2.

Таблица 2.2 — Значения виброперемещения и техническое состояние

Частота вращения, мин-1	Амплитуда виброперемещения, мкм
	отлично	хорошо	удовлетворительно	требует исправления	опасно
300	0-27	27-70	70-140	140-260	> 260
500	0-25	25-60	60-125	125-240	> 240
600	0-22	22-56	56-118	118-240	> 230
1000	0-18	18-45	45-100	100-200	> 200
1500	0-15	15-40	40-85	85-170	> 170

Измерение общего уровня вибрации

При определении значений общего уровня вибрации проводят измерение среднеквадратичного значения виброскорости в частотном диапазоне 10-1000 Гц. Это соответствует требованиям стандарта ИСО 10816. Регламентируется проведение измерений в трёх взаимно перпендикулярных направлениях: вертикальном, горизонтальном и осевом. При нормальной работе горизонтальная составляющая имеет максимальное, а осевая — минимальное значение. Виброскорость для большего количества механизмов не должна превышать 4,5 мм/с.

Значения виброскорости, определяющие границы состояний:

• до 4,5 мм/с — удовлетворительное;
• 4,5-10,0 мм/с — плохое;
• свыше 10,0 мм/с — аварийное.

Значения приведены для работы под нагрузкой.

Для оценки состояния подшипников качения проводят измерения пикового и среднеквадратичного значений виброускорения в частотном диапазоне 10-4000 Гц. В общем случае:

• хорошее состояние характеризуется значением пикового значения виброускорения — до 10,0 м/с²;
• удовлетворительное состояние — среднеквадратичное значение не превышает 10,0 м/с²;
• плохое состояние наступает при превышении 10,0 м/с² среднеквадратичного значения;
• если пиковое значение превышает 100,0 м/с² — состояние становится аварийным.

Одним из признаков наличия значительных повреждений является присутствие в спектре виброускорения составляющих со значениями свыше 9,8 м/с².

< 2.2. Шумы механизмов

Содержание

2.4. Контроль температуры механизмов >